The Twelve Marbles Problem
Time to read: 6 min read
# Problem Premise
You have 12 visually-identical marbles, however, while 11 of the marbles have the same weight, one marble has a different weight than the different marbles (it can be either heavier or lighter). You want to find which marble is the one with the different weight.
The difference in weight between the special marble and the other 11 is too small to be discerned by hand, so you have decided to use a scale (the old-fashioned balance kind where you place a weight on either side and the heavier side drops). You can only use the scale three times; how can you determine which marble is the odd one out?
# Solution
My initial thought process was to try to get rid of the largest percentage of marbles after each weighing, however, it quickly became apparent that there isn't enough information to determine the marble in only 3 weighings. After some trial and error I came upon the actual solution:
- First seperate the 12 marbles into three groups of 4 marbles each. Within each group, further divide the marbles into a subgroup of 3 marbles and a subgroup of just 1 marble.
 The Grouping of the Marbles
The Grouping of the Marbles
- Weigh marble group A with group B and we get two cases:
Case 1: If group A and group B balance then we know that the irregular marble is in group C. We weight C1 with A1 (or B1) and we get two subcases:
Subcase i: If the C1 and A1 are balanced, then the marble C2 must be the irregular marble.
Subcase ii: Since we know the marbles in A1 are all regular weight, if C1 is heavier/lighter than A1 then we know the the irregular marble is in C1. We can weigh any two marbles in C1 together; if the two marbles are equal then it must mean that the irregular marble is the third marble in C1. If the two marbles do not equal, and since we know that the irregular marble is heavier/lighter than the others, we can identify the heavier/lighter marble as the irregular marble.
Case 2: If group A and group B do not balance then we know that the irregular marble must be in either A or B, and that all marbles in C are regular. WLOG we assume that A is heavier than B. This is the interesting part of the problem; we use C to determine which subgroup contains the irregular marble. We swap either A1 or B1 with C1, and for the non-swapped group, we swap the singly-grouped marble in that group. For example, we can weigh C1 + B2 against B1 + A2. We get three subcases:
Subcase i: If C1 + B2 and B1 + A2 balance, then it must mean B2, B1, and A2 only contain regular marbles. The irregular marble is thus in A1. We can compare any two marbles in A1, and if they are equal, the third marble in A1 is the irregular marble. If the two marbles are not equal, since we know from our first weighing that A is heavier than B, we know the irregular marble must be the heavier one.
Subcase ii: If C1 + B2 and B1 + A2 is unbalanced and C1 + B2 is heavier than B1 + A2, then B1 is too light. We know this because A1 + A2 is heavier than B1 + B2, so A1 cannot be too light and B2 cannot be too heavy. If A1 is too heavy or if B2 is too light then C2 + B2 cannot be heavier than B1 + A2; A1 and B2 are thus regular marbles. We can compare two marbles within B1 and determing the irregular marble.
Subcase iii: If C1 + B2 and B1 + A2 is unbalanced and B1 + A2 is heavier then either B2 is too light or A2 is too heavy. We know this because A1 + A2 is heavier than B1 + B2, so B1 cannot be too heavy. B1 likewise cannot be too light, since C1 + B2 would then be heavier than B1 + A2; the marbles in B1 are thus regular. We can compare either A2 or B2 with C2 and determine the irregular marble.
This puzzle took me a couple of minutes, but I think the best approach is to keep envisioning different cases (almost like "if-statement" clauses) to whittle down the uncertainty.
One way to quantify the uncertainty is with entropy, a concept from information theory. One can classify marbles into two categories: those which we can determine (D) and those which are undetermined (U). We can calculate entropy with D and U. The formula is as follows:
For our scenario we care about:
The lower the entropy, the less uncertainty there is within the system. The goal is thus to get the entropy as low as possible. In this case, at the beginning, D = 0 and U = 12, so P(D) = 0 and P(U) = 1. You may have noticed that when we plug those figures into the entropy formula, the entropy is actually already 0 (yes, technically
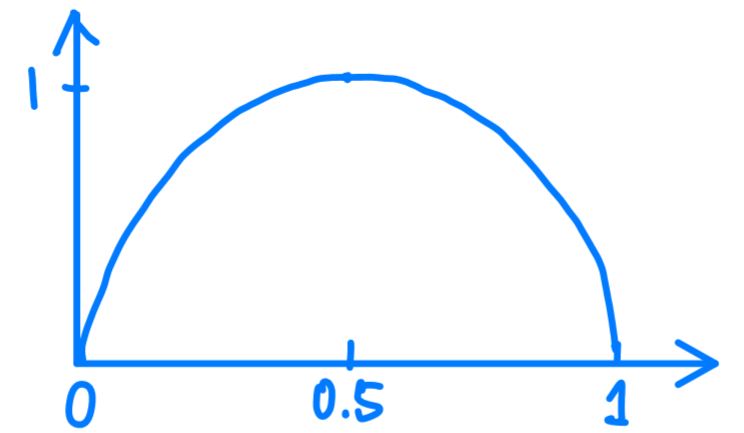 The Entropy of p and (1-p)
The Entropy of p and (1-p)
If the x-axis is P(D), then at the beginning, we are on the leftmost end (when we have determined nothing) and our goal is to get to the rightmost end (when we have determined everything). The opposite is true if the x-axis is P(U).
While the entropy conceptualization of the question is unnecessary for our 12 marbles; when we scale the complexity of the problem (maybe hundreds of even thousands of marbles), we can use this framework to algorithmically solve the problem. We can solve the question by searching through possible states, perhaps using some sort of heuristic search, such as A*, or even some sort of reinforcement learning. This conceptualization makes for an interesting optimization problem.